[gview file=”http://oafak.com/wp-content/uploads/2019/08/Week-Four.pdf”]
There are a number of examples in the text that today’s lecture expects you to type in and practice. If in future, you do not know how to program, it will be because you were lazy in simply typing in code and running them. “The fault, dear Brutus, is not in our stars,
But in ourselves, that we are underlings.” A word enough for the wise!
There is a test next week on Chapter One. Those who refuse to practise are going to have a cold shower on a harmattan morning!
Good day sir, please how can we access the textbook?
Find it here
Good day sir,
page 70 solved problem 1.3
according to the tell tale signs
A dummy index must occur twice. But it DOES NOT have to occur in another term.
but in the solved problem we have
× = k
a*b = eijk aj bk ek
i know from Vector Product in Component Form that
× = k
ei * ej = eijk ek
aj is correct also but the bk i think it should be bi and not bk.
i dont know if am the one getting it wrong but according to the tell tale sign if am to solve that problem the results would be
a * b = eijk aj bi ek
the tell tales sign 3 made a *b = eijk aj bk ek wrong to me dont know if it is correct sir.
or a*b = ejik aj bi ek
Eniola, it is a typo error.
It should read a×b=eijk aj bk ei
Dr Adewumi’s comments are correct. The text will be corrected.
from solved problem 39 the result of ⋅ ( ⊗ ) is a vector.
from solved problem 40 the result of × ( ⊗ ) is a tensor.
I don’t understand how this was simplified to result in a vector and tensor respectively.
from solved problem 39 the result of u ⋅ (v ⊗ w) is a vector.
from solved problem 40 the result of u × (v ⊗ w) is a tensor.
I don’t understand how this was simplified to result in a vector and tensor respectively.
The first expression, when fully expanded in component form is the same as (w⊗v)u which is obviously a vector. The tensor nature of the second expression will become more obvious to you when we are deep into the next chapter.
Good Morning sir,
Tried the mathematica codes on page 12 and kept getting error
First no arrow automatically appeared after typing Plot range and Ticks but was able to bypass that with a cut and paste trick collecting arrow from Plot Style But it still didn’t run.
It said
Visualisation’Core’ParametricPlot3D: –Message text not found — ({1, y, z, Null})
General : further Output of Visualisation’Core’ParametricPlot3D::invfuncs will be suppressed during this calculation
And so many more
To give me a copy of your code so I can see your problems is doable. We are NOT at that point yet. The way to type in the arrow is to follow the minus sign with > (the “greater than sign”, above the period sign). You are at the first step of simply copying my working code and getting the pain of executing it while hunting down your typos. I have typed the code in just now without changing anything. It works just fine. I will urge you to go back again and compare what you typed to what was given. The code works fine!
Solved problem 1.16,page 78… Anybody can help with how they got to the next step of the solution(the part I wrote the note)
1.16 Show that ( × ) ⋅ ( × ) × ( × ) = ( × ⋅ )^2
( × ) ⋅ ( × ) × ( × ) = ( × ) ⋅ [( × ) ⋅ ] − ( × ) ⋅ [( × ) ⋅ ]
I don’t really get Wat happened here….seems to me like a part of the equation was just taken
= ( × ) ⋅ [( × ) ⋅ ]
= ( × ⋅ )(( × ) ⋅ )
= ( × ⋅ )( ⋅ × )
= ( × ⋅ )^2
Nice content
170404529
Good afternoon sir. I have a question regarding equation(65) in page 39 of Chapter 1. I do not understand why
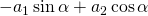became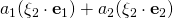 
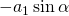became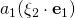 
Especially how
Hello Oyepeju,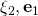
and 
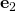are unit vectors. Computing their scalar products is now a matter of knowing the angles between the pairs of them. Back to the graphics, you find that the angle between 
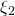and 
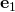is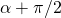 
while the angle between 
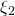and 
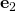is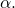 
Now remember that
Before I take on your question, let me commend you on the the Latex coding you did. I leave the edited code at the end to show you the few changes I made so that we can continue communicating this way with ease. Please note that the beginning of Latex is not the double dollar sign here but [late x], the end is [/late x]. In what I typed, I deliberately put a space into these delimiters to prevent the code from creating the equations in order to show you the raw code.
Now to your question:
Notice that
(1)
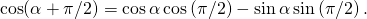
Do I need to remind you that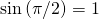
and that 
?
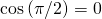Your latex input corrected: [late x] -a_{1}\sin\alpha + a_{2}\cos\alpha [/late x] became [late x] a_{1}(\bold{\xi}_{2} \cdot \bold{e}_{1}) + a_{2}(\bold{\xi}_{2} \cdot \bold{e}_{2}) [/late x]
Especially how [late x] -a_{1}\sin\alpha[/late x] became [late x] a_{1}(\bold{\xi}_{2} \cdot \bold{e}_{1}) [/late x]
Good evening sir.I was going through chapter 1 again and I saw that I didn’t understand how we arrived at equation 61 under coordinate transformation .Please I will really appreciate if you can explain sir.
Once you realize that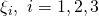
as well as 
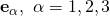are sets orthonormal vectors, then the scalar products will always lead to Kronecker deltas: 
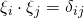, and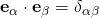 
. Use the substitution property of the Kronecker deltas and the fact that scalars can be carried along as they move around the equations; there is nothing really difficult in equation 61. If you have any particular step you can still not follow, let me know.
Good day sir, (a+b).(a-b)x(b+a)
The first two terms yields the difference of two squares ||a||^2 – ||b||^2 how can the last term (b+a) act on it
160407013
In a triple product, you are NOT allowed to perform the dot products first! That principle is elementary and it is the reason why we do not bracket off the cross products because the order of the products obviously starts from the vector product! Overcome that deficiency in your knowledge and use the result in Q1.4b. Notice that you can swap the cross and the dot without changing the result:
(1)
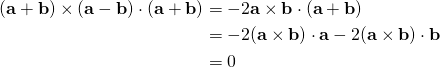
The last equality coming from the fact that triple products of linearly dependent vectors vanish. If we write the original question as,
(2)![\begin{align*} \left[ \bold{(a+b),(a-b),(a+b)}\right] \end{align*}](https://oafak.com/wp-content/ql-cache/quicklatex.com-41835177a10cbf517b8f3701c915ba63_l3.png "Rendered by QuickLaTeX.com")
we can conclude right away that the answer is zero because of linear dependence! No need to expand at all!