Here are the slides for the second week.[gview file=”http://oafak.com/wp-content/uploads/2019/08/Week-Two.pdf”]
I note that there have been no comments or questions from Systems Engineering students. There will be a test two weeks time on the first four weeks. Those who do not practice the Q&As as instructed will have themselves to blame.
Good day sir,
Please I don’t understand the component form of vector product in the textbook sir pages 31 and 32.
“I don’t understand…” is not a question. It is a comment that is not actionable. While I desire comments and questions, this particular one cannot be helped. You can tell me where you followed the notes up to and at what particular step you have an issue. If there are ten steps in an issue, “I don’t understand can mean anything from “I do not even know what the issue is all about”, or “I do not follow step 8”! The ball is still in your court to become more specific in what in the component form you have difficulty with.
Thank you sir. I have understood it now. I rushed through it instead of reading it calmly sir. The slide helped me.
Very happy to know your problem is solved. Please ask your quetions after you have read what you already have. I am always available to assist you.
Good day.
from question 1.16 of the textbook “Chapter-1.-Review-of-Vectors-1”
(a × b)⋅(b × c)x(c × a) = (a × b) ⋅ [(b × c)⋅a]c − (a × b)⋅[(b × c)⋅c]a
= (a × b) ⋅ [(b × c) ⋅ a]c
= (a × b ⋅ c)((b × c) ⋅ a)
= (a × b ⋅ c)(a ⋅ b × c )
= (a × b ⋅ c) 2
from line 4 of this comment, (a × b)⋅[(b × c)⋅c]a = 0
please can i get a further break down of this
The triple product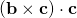 is a scalar quantity; call it
is a scalar quantity; call it 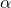 . (You should be able to see, after you have read to the end of this comment that
. (You should be able to see, after you have read to the end of this comment that 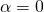 ). Your expression is therefore,
). Your expression is therefore, 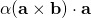 . This scalar triple product vanishes for at least two reasons:
. This scalar triple product vanishes for at least two reasons: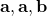 which vanishes because of linear dependency of the vector edges.
which vanishes because of linear dependency of the vector edges.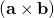 is perpendicular to
is perpendicular to 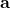 . Taking its dot product with a brings in the cosine of 90 degrees. You know what that means.
. Taking its dot product with a brings in the cosine of 90 degrees. You know what that means.
1. It is the volume of a parallelepiped with sides
2 The vector
Watch out for such simple applications of elementary knowledge.
Thank you sir
Good day sir.
Products of Alternating tensors.page 30
when we are expanding the matrix from page 30.
11 + 22 + 33i
i was trying to break it down myself using the Kronecker Delta the answer is dri.
but when i broke it down i had dri + dri + dri so am thinking there should be a 3 before the final answer dri.
Trying to copy and paste formulas and symbols from the textbook doesnt show on this website maybe something can be worked out on the site sir.
the 11 +22 + 33i
is dr1d1i + dr2d2i + dr3d3i.
Sir,in page38, I don’t understand how equation61 came into play.
which part there is it where the Kronecker Delta acted as a substitution symbol?
we have 6 parts there which one exactly or all?
Eniola, for the Kronecker delta to ack as substitution symbol, it MUST share an index with another symbol. In that case remove the Kronecker delta and replace the unshared index of the other symbol. It is easier done than explained. Look at the examples in class and in the book.
Ayomide, Look on the previous page, you see the expression for aij. as for bij, you will need to take the dot product of equation 59 with xi alpha to get it. Ask me in class if its still unclear
Good day sir, from practice question 1.20
please sir can you explain? what happened to “![Rendered by QuickLaTeX.com - [(\mathbf{w} \times \mathbf{u}) \cdot \mathbf{w}]\mathbf{v})](https://oafak.com/wp-content/ql-cache/quicklatex.com-8dbf6b748b3da9086c47e7d32789445f_l3.png) ”
”
that the next line became
Ajibola Areo
170407512
Systems Engineering
For the term![Rendered by QuickLaTeX.com \left[\bold{w,u,w}\right]](https://oafak.com/wp-content/ql-cache/quicklatex.com-12a47c4c62b5d6d5bb3f18bab9bde0c0_l3.png) observe that you are taking the triple product of three vectors that are linearly dependent. Looked at in another way, you are looking at the volume of a parallelepiped where two sides are the same vector! Such a parallelepiped will be on a plane – giving you a zero volume!
observe that you are taking the triple product of three vectors that are linearly dependent. Looked at in another way, you are looking at the volume of a parallelepiped where two sides are the same vector! Such a parallelepiped will be on a plane – giving you a zero volume!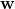
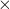
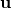 and
and 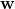 , remember that
, remember that 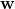
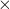
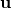 is perpendicular to
is perpendicular to 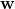 and that the scalar product of two perpendicular vectors is zero.
and that the scalar product of two perpendicular vectors is zero.
If you want to look at it as the dot product of
Thank you sir
Sir, When I was reading some notes under the Levi Civita symbol. I came upon the word Abelian.
Sir, what does it mean for a set of operators to be Abelian
Which notes are you referring to? Let your reference be specific.