The site for the course is www.s2pAfrica.org the notes and other materials for the course are also there. Until further notice, reach me here for immediate answers to your questions. We are still organizing that site.
Here are the slides for the opening class:
[gview file=”http://oafak.com/wp-content/uploads/2019/07/Week-One-.pdf”]
The following is the Course text.
[gview file=”http://oafak.com/wp-content/uploads/2019/07/Chapter-1.-Review-of-Vectors-2.pdf”]
Required Preparation for Next week: Read Pages 23 to 50; Work Examples 1-25 in the Solved Problems Section.
Ask your questions online so that other students may benefit from your insight and the answers you get.
Good day sir,
This question may not relate to the course but i have always have it in mind.
As an engineer with a lot of experience in your field what do you think a systems engineer should be able to do as soon as he graduates.
I mean i can simply tell a person am a sytems engineer and they continue to question me thoigh i have answers which i go on google and give but i would like to know from your own perspective.
Thank you sir.
What Eniola Olaleye will be able to do immediately after graduating are exactly the same things Eniola Olaleye was able to do immediately before graduation. The transition is NOT sudden. It is gradual.The certificate is an over glorified piece of paper!
Any engineering curriculum is a combination of a number of skills packed together to call a name. What it actually is depends on a number of factors. One of these factors is the kind of people that taught you, what they are good at, and how much of that you allow yourself to learn.
Here in our department, there is Artificial Intelligence and Robotics. We also have Engineering Design and Analysis, we have some amount of Operations Research and Industrial Engineering. Any of these can fetch your daily bread. None of us knows what you will do. The strategy in any engineering training is to expose you to as much as we can while you are here. Your certificate, by itself is not going to make you do anything.
Let me give you an example: Up to 10-15 of my colleagues here at Unilag went into Oil companies after graduation. Shell took a number of them: Mechanical, Civil, Computer Science, Physics, etc. There, they were exposed to similar things in groups to allow each to develop their talents. Guess who became the boss? Not the Mechanical Engineers, Not the Chemical Engineers, Not the Geologists! Who? the computer scientist! He became head of the organization! When you talked to him several years later, he was no longer a computer scientist! He had allowed himself to learn a number of things.
Many of our graduates have become so successful in software and are making waves there. It is not inevitable; it is what was emphasized to them that they took to.
The reason for Continuum Mechanics is that it gives you a wide view. However, you must get that into something specific for yourself that interests you. The wide knowledge is good; it MUST be consummated into some specific things to be of any use. We offer you a lot of skills that you can develop. If you want marks, you get what you are looking for. If you want skills then go for them and you will be able to do things that people will not even remember what you studied!
The software knowledge you gain in modelling can be useful in many ways. My goal is to train you to be aware of your environment, see how you can interact with it using your engineering knowledge and make a difference. Whether you will be able to do that or not is not because you are “doing systems engineering”! No matter what you do, engineering is engineering. There is nothing, for example, stopping you from understanding microprocessors like an electrical engineer or ceramics like a Metallurgist! They are all before you as the basic training is essentially the same. If you CPPF, then you have wasted your life in the university!
Good day sir
Please I have a question as regards the problem set we were given…
If I am to use index notation to prove that det C = det a*det b.
Where a and b are both 3 x 3 matrix.
Am I to use the kronecker delta.. and how .
I am very confused.
There is an easy proof of this in Chapter Two that does not involve the Kronecker delta at all. You will not even need to break the tensors into component form. But please identify which class you are in to get further assistance.
I am in Mechanical engineering
Year 3.
Ugochukwu, the first thing you can do is start from what you know. (1) write out the full form of matrix A (2) You already know how the find the determinant of a matrix, so write it out (3) Look out for the pattern the subscripts take and ask yourself “Can I write this in a compact form using knowledge gained from what was taught in class and my private reading?” (4) Try it out. The objective of this question is to make you work from what you know to new concepts learnt in the last class. By the time we get to chapter two, you will learn an easier way to prove this. But for now, use what you learnt in the last class to crack this question.
in the product of the alternating symbol,if they have no common indices,can any two index be picked?
Holy Boy! If there are no common indices, leave the product as is. Do not touch!
Nice book so far
Good pm sir,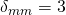 ) but if it is substituted; it will disappear (more like 1).
) but if it is substituted; it will disappear (more like 1).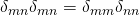 )
)
it was said that if the indices of the Kronecker delta appear the same naturally, it will be equal to 3(
My question is; if after substituting a Kronecker delta both now have the same indices each, what will be the result?
e.g (
They are not the same. First, you will need to go back to the definition and see that what you are posing cannot be correct. For example,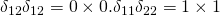 . All I have just done is to simply substitute
. All I have just done is to simply substitute 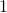 for
for 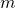 and
and 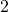 for
for 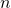 in the way you have posed the question. That is not even the end of story. Because of the repetition of indices, there is an implied summation. Hence,
in the way you have posed the question. That is not even the end of story. Because of the repetition of indices, there is an implied summation. Hence, 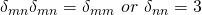 whereas as there are no shared indices between
whereas as there are no shared indices between 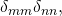 each of them sums to 3 and the product sums to 9! For these two reasons, a small thinking shows that on any account, it should have been obvious that your posed question is not tenable simply from the application of the definition and elementary principles!
each of them sums to 3 and the product sums to 9! For these two reasons, a small thinking shows that on any account, it should have been obvious that your posed question is not tenable simply from the application of the definition and elementary principles!
Good evening Sir.
I am having a problem when confirming the equivalence of the Tensor product.
It is defined on page 19, that the tensor product of vectors a and b acting on another vector c is equivalent to (b.c)a
On using Mathematica to check this
If @ represents the dyad symbol
( a@b)c and (b.c)a gave me different answers
The former, a matrix and the latter, a vector.
…………………………
But when I dotted c with the Tensor product of a and b,
I.e ( a@b).c,
it gave me the same answer(a vector) with (b.c)a
I do not understand what I had to ‘dot c’ before the definition stands true by mathematica
I am assuming you used the function TensorProduct[] in Mathematica. Mathematica provides for vectors and tensors using the same syntax as in Matrix analysis. The rules of Mathematica are NOT identical with the syntax we adopted in tensor analysis. That is why in places such as tensor products and contractions, it is necessary to use the dot because Mathematica cannot correctly interpret the product otherwise. Do not forget that you did not supply a tensor to Mathematica! All you supplied was the matrix of the tensor! You run the last mile of interpretation. I think you are doing well.
This was insightful.
Thank you sir.
I do not understand why* I had to ‘dot c’ before the definition stands true by mathematica
Already answered
Good day sir,
page 71 in the text book
question 1.6
Given that for any vector , × = × , Show that =
We are given that ∀ ∈ , × = × , Now take a dot product with , we have that, ⋅ × = ( × ) ⋅ = 0 = ⋅
when we take a dot product with a we had this
⋅ × = ( × ) ⋅ which is not clear to me sir.
a.b * v = (a*b).v
this
Remember that the scalar triple product is unchanged if we swap the dot and the cross. We used that fact here. Furthermore, note that the product is zero because![Rendered by QuickLaTeX.com \bold{a}\cdot\bold{a}\times\bold{b}=\left[\bold{a,a,b}\right]](https://oafak.com/wp-content/ql-cache/quicklatex.com-930af45c59ac3fcc09c8beff3b372688_l3.png) vanish because of linear dependence on the LHS. I think the rest of the explanation is straightforward.
vanish because of linear dependence on the LHS. I think the rest of the explanation is straightforward.
Already answered
Hello sir,
Question 1.3 in the Chapter 1 Q&A is a bit confusing. How does the expression equal zero?
Good afternoon sir,
In Page 70, Question 1.3
The explanation after the solution says “The expression in symmetrical in i and j, it is also anti-symmetrical in the same two
indices at the same time. The same situation occurs on the RHS”
Is it meant to be symmetrical twice or anti-symmetrical twice
And what would it mean with respect to i and j
If a term is symmetrical in two indices, it means a swap between these two will leave the value intact. If is is antisymmetrical, a swap will change the sign. Therefore, when a term is symmetrical as well as antisymmetrical in the same indices, it means that term equals the negative of itself. This is only possible if the term is zero.
Your interpretation is wrong. There is NO indication of “symmetrical twice” at all! This is a term you have invented and did not come from the book nor the slides!
Good morning Sir,
I really wish there was a way we could have the ability to attach images to our comments, that way we would be able to show you our problems more accurately
You do not need to generate the arrows. Simply type minus sign followed by the > (above the period key). It may or may not immediately convert to an arrow, but it will work fine.
Sir, how does one identify explicitly that a term is symmetric? Is it just due to the fact that it has a variable repeated twice over 2 indices? as seen in chapter1 Q1.30
I just saw the reply to my Question…thank you for the platform
Hello Mustapha,
You are welcome to the forum. Happy that you posted a question. I am really glad that some of the questions are answered by other students. These provide a corpus of educational materials that all can learn from.
From page 50,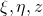 , I obtained instead
, I obtained instead 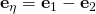 and
and 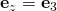
Upon differentiating the position vector for the parabolic cylindrical coordinate system with respect to the coordinate variables,
Your differentiation is in error. I made a sign error in the second base vector. For the position vector,
(1)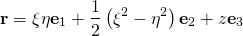
the correct result after differentiation is:
(2)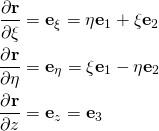
Upon differentiating the position vector for the parabolic cylindrical coordinate system with respect to the coordinate variables,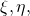 I obtained instead
I obtained instead 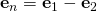 and
and 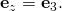
Already answered.
In page 51 of chapter 1, We treated real vector spaces but mentioned about a complex number space being possible. My question is that will a complex number 3D vector space constitute the complex independent or three independent variables in which one or two may be imaginary
I am not personally acquainted with the use of such a vector space.
Good evening sir,
Concerning chapter one, I noticed that in the indical notation of your cross product,you followed the order (i,j,k) while in some questions you followed (j,k,i).
Why is that sir?
Reference:Questions 1.2,1.3,1.32
Your questions will not arise if you learn the meaning of the Levi-Civita symbol! Where have you been all the while?
Look at slides 2.25-2.27