In this last week of lectures before your second test, we shall be looking at the Eigenvalue problem you have encountered already in your Engineering Mathematics. There is an equipollency between the tensor eigenvalues and those of matrices. The issues here are therefore familiar. The tensor form has specific physical implications in our engineering courses especially as it relates to the Principal invariants of tensors and the spectral form using eigenbases.
We shall also have two tutorial classes on the worked examples to help prepare you for the test. Remember that the test is a paraphrase of the same problems that are solved for you in the Q&A at the end of each chapter. EVERYTHING in the Q&A is part of the questions populating the database from where your questions are drawn.
[gview file=”http://oafak.com/wp-content/uploads/2019/09/Week-Nine-1.pdf”]
For the triple product of the vector differences using the order method where we had to follow a specific pattern to solve it(111,112….) I didn’t understand how the signs alternates or the basis of knowing which sign to place to get the solution.
The signs did not alternate! Simply take a look at what you are multiplying on a case-by-case basis! Or, even more simply, assume they are scalars, will the product of a1, a2 and -b3 (112) not have a negative sign? Will the product of a1, -b2 and -b3 (122) not have a positive sign? Do not simply look at these things! Write them out! Work them out!
In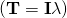
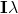 tensor is a negative 1 (-1)
tensor is a negative 1 (-1)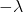 takes any position where 2 is
takes any position where 2 is
Using 111,112,121…
Because the coefficient of the
Since
If you have 2 once it is negative
If you have 2 twice (- times – = +)
If you have 2 trice then (- times – times – = -)
Naomi Inyang
170407509
Systems Engineering
Is it lambda that you are trying to write? All you need to do is to write [late x]\lambda[/late x] just don’t put the space I deliberatly added before the x!
The statement: “Tensors are not matrix!”, as crystal clear as it is, I should say is not meant for a mind or brain that do not understand fully what tensors are even if he/she fully fathoms the principles of matrix. Am saying this because we just accepted the statement for the fact that it was said by a Professor without really thinking deep about the intuition behind the statement in the first place.
Me as a typical example, studying about tensor and constantly doing all scalar computations based on matrix but continuously telling my self that “tensors are not matrix!”. Unlike the different types of zeros which is now pretty clear to me I still find the basic fact of tensors not been a matrix challanging.
I tell myself these sir:
– Matrix is a kind of tensor ( 2nd Order) with the expection that it has an additional divison axiom.
– Tensors is a matrix with a exception of dyads.
My question sir, is that, is it the division operation and the dyad representation that made a matrix not qualified to be a second order tensor sir?
A vector is a first-order tensor, once a coordinate system is chosen, its components can be expressed as a column or row matrix if you ignore the basis that are needed to fully define it. Most of your computations, after we have agreed on the coordinate system we are using, are equipollent. Mathematica, for example, uses the same matrix operations for tensor operations because of that. Further, a second-order tensor has, for its components, on a chosen set of basis vectors, a matrix form that is like a three by three matrix. Again, you leave the dyad bases out of the comparison. If you take it into consideration, the difference is clear! (See Slides 38-39, Week 3 for vector and dyad full component representations in Cartesian Coordinates). By the time you get to a third-order tensor, there is no direct matrix representation because it will require a three dimensional arrangement of numbers even leaving out the triad bases. You can go on this way to fourth, fifth, sixth and eighth-order tensors that have physical meaning. I am unable to conceive the use of tensors of orders higher than eight even though they can be defined. So, on the basis of the components alone, tensors differ from matrices because you must add their bases to fully define them. When orders are higher than two, the matrix representations begin to break down.
If you now leave the comfort of the Cartesian system and start changing bases to curvilinear orthogonal and non orthogonal systems, the differences become more glaring. You will begin to see that, while any arrangement of numbers can be a matrix, tensors have specific transformation characteristics that define them. These rules are what make them tensors not just the fact that they are numbers in a structural relationship. At the beginning of chapter 2, we had certain transformations that can be represented as matrices; yet they are not tensors!
We can say more. The similarity between matrices and tensor components are good for us. However, those who understand the differences will be able to achieve more with either. Most of what is there to know about tensors are at the second-order where the equipollency with matrices is quite advantageous. The bases and the transformation rules are two major issues that distinguish tensors even when they have similar representations. Yet tensors go to levels beyond regular matrix representations.
Apart from the differences we have described, remember that a tensor is more than its components! Whether you express the tensor in component form or not, a tensor exists! For example, a stress tensor exists in a loaded body whether someone decides, for analytical purposes, to analyse it via its components in the Cartesian system. The analyst sees the matrix of the tensor and its Cartesian basis dyad set. Another analyst looks at the same tensor from a different perspective. He is still looking at the same tensor object. Now the matrix is different, the dyads are different yet the tensor remains unchanged. This transformation that connects the dots, ensure we are still talking about the same quantity, even though it is presenting itself as different matrices, is the fundamental character of a tensor. It is the transformation rules that makes it a tensor.
Of course, you can say that there are transformation matrices. Yes, that is true. But they are not the essential definition of what matrices are!
Well noted Sir
In the text sir, page 19 of Chapter II Tensor Algebra Continuum Mech, or on slide 25 properties of tensor II,![Rendered by QuickLaTeX.com T_{ij}^c=\frac{1}{2} e_{jmn} {\bold e}_i \cdot [{\bold T}^c ( {\bold e}_m \times {\bold e}_n )]](https://oafak.com/wp-content/ql-cache/quicklatex.com-2c646696c8dc58d794ce7e39516bb016_l3.png)
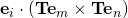 seeks the
seeks the 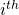 component of the vector
component of the vector 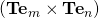 , just like that of the component finding of vector sir. Even as I know that
, just like that of the component finding of vector sir. Even as I know that 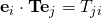 and that
and that 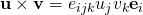 , I still do not understand why you chose to bring in the solution
, I still do not understand why you chose to bring in the solution 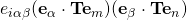 sir?
sir?
You said the expression
And why can’t we use this format sir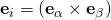 then replace
then replace 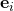 to get
to get 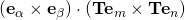 and this eventually gives
and this eventually gives 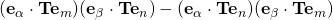 sir?
sir?
First of all, let me begin by commending your effort to understand the lecture and the tedious (not difficult) tensor and vector objects that we deal with here. It is good to start with the factual errors in your post before I answer the real question that you have asked. I will enumerate: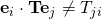 ! The correct thing is that,
! The correct thing is that, 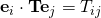 .
.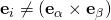 . Instead, looking at Week Two, Slide 33, you find that,
. Instead, looking at Week Two, Slide 33, you find that, 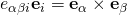 . And, if you want to transfer the Levi-Civita to the other side,
. And, if you want to transfer the Levi-Civita to the other side, 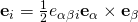 . (Eqs 45-46, pg 32 Chapter One). Using this expression would have led to the same solution in more steps. Furthermore, your equation can be faulted under the grounds of indicial inconsistency. If all your indices are free indices (not dummy, since they are not repeated), they MUST be present in each term! See that the correct representation DOES NOT suffer any such sickness!
. (Eqs 45-46, pg 32 Chapter One). Using this expression would have led to the same solution in more steps. Furthermore, your equation can be faulted under the grounds of indicial inconsistency. If all your indices are free indices (not dummy, since they are not repeated), they MUST be present in each term! See that the correct representation DOES NOT suffer any such sickness!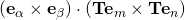 leading to
leading to 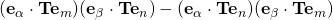 was used under a wrong premise. This result, called Lagrange Identity, was derived in Q1.24; when used correctly, we arrive at the same answer as follows:
was used under a wrong premise. This result, called Lagrange Identity, was derived in Q1.24; when used correctly, we arrive at the same answer as follows:
1. Alas,
2. Again,
3. Lastly, your scalar product over vector product expression is correct; I commend you on that, but the correct result
(1)![Rendered by QuickLaTeX.com \begin{align*} &\frac{1}{2} e_{jmn}\bold{e}_i \cdot ( {\bold {T e}}_m \times {\bold {T e}}_n )\\ &= \frac{1}{4} e_{jmn}e_{i\alpha\beta}(\bold{e}_\alpha \times \bold{e}_\beta )\cdot ( {\bold {T e}}_m \times {\bold {T e}}_n ) \\ &= \frac{1}{4} e_{jmn}e_{i\alpha\beta} \left[ ( {\bold e}_\alpha \cdot {\bold {T e}}_m )( {\bold e}_\beta \cdot {\bold {T e}}_n )- ( {\bold e}_\alpha \cdot {\bold {T e}}_n )( {\bold e}_\beta \cdot {\bold {T e}}_m ) \right]\\ &= \frac{1}{2} e_{jmn}e_{i\alpha\beta} ( {\bold e}_\alpha \cdot {\bold {T e}}_m )( {\bold e}_\beta \cdot {\bold {T e}}_n ) \end{align*}](https://oafak.com/wp-content/ql-cache/quicklatex.com-36c023c67d0e61a1fc8bd65a8f4ccd9f_l3.png)
which is the same result as in the text. There are three extra steps as you can see. The last equality could have been taken in two additional steps, making five.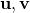 , the vector product,
, the vector product, 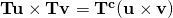
We used the fact that, for any two vectors
Now to the question: Why was it necessary to bring in the solution,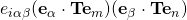 at this point? It became necessary to introduce new indices to avoid conflict with
at this point? It became necessary to introduce new indices to avoid conflict with 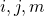 and
and 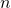 that are already used! In finding the
that are already used! In finding the 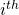 component of the product of two vectors, remember that the vectors themselves were obtained by operation on vectors by the tensor
component of the product of two vectors, remember that the vectors themselves were obtained by operation on vectors by the tensor 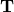 . We introduce the
. We introduce the 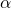 and
and 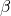 components of those operations since it really does not matter what components we chose: they will end up in the dummy variables anyway. We only had to avoid already used variables for the new dummies: We chose two indices,
components of those operations since it really does not matter what components we chose: they will end up in the dummy variables anyway. We only had to avoid already used variables for the new dummies: We chose two indices, 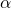 and
and 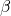 that were NOT yet used at that point. If you chose any other indices than
that were NOT yet used at that point. If you chose any other indices than 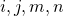 , you would still arrive at the same answer. It is just those that MUST be avoided to move on.
, you would still arrive at the same answer. It is just those that MUST be avoided to move on.
Before i go further seeking solution to why i am here,sir.I would like to point out that i have gone through a few of the solved examples and based on every lectures we have had so far and understanding the rules guiding each steps.It is hard to say i am not familiar to what is going on in between these steps but the problem here is the approach to each of these examples and how to interprete them from the on set.This, i will like you to emphasize on come tomorrow tutorial class.
Now,back to the real question…
in the text sir ,chapter 2-Tensor Algebra-example 2.8
can you give a detailed explanation on how this [(× )⋅] vanished from the equation below
× =(× )×(× ) =[(× )⋅]−[(× )⋅]
=[⋅ (×)]=(⊗)(× )
I think this question is already answered below.
Before i go further seeking solution to why i am here, sir. I would like to point out that i have gone through a few of the solved examples and based on every lectures we have had so far and understanding the rules guiding each steps. It is hard to say i am not familiar to what is going on between these steps but the problem here is the approach to each of these examples and how to interpret them from on set. This, i will like you to emphasize at tomorrow’s tutorial class.
Now, back to the real question:![Rendered by QuickLaTeX.com \bold{[(w \times u)\cdot w]v}](https://oafak.com/wp-content/ql-cache/quicklatex.com-4346dba8c0fb17708641e9f38a611314_l3.png) vanished from the equation below
vanished from the equation below
In the text sir, Chapter 2-Tensor Algebra-Example 2.8, can you give a detailed explanation on how this
(1)![Rendered by QuickLaTeX.com \begin{align*} \bold{x} &=\bold{(w \times u)\times (w \times v)}\\ &=\bold{[(w\times u)\cdot v]w - [(w \times u)\cdot w]v} \\ &= \bold {[w \cdot (u\times v)]w=(w\otimes w)(u \times v) } \end{align*}](https://oafak.com/wp-content/ql-cache/quicklatex.com-0ea4fe35596a56e1ef4e702a1a41159f_l3.png)
Your comment and request are noted. The answer to your question is straightforward as you can see:![Rendered by QuickLaTeX.com \bold{[(w \times u)\cdot w]v}](https://oafak.com/wp-content/ql-cache/quicklatex.com-4346dba8c0fb17708641e9f38a611314_l3.png) note that
note that 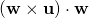 is the scalar products of the vector result of
is the scalar products of the vector result of 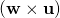 and
and 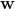 . These two are perpendicular vectors! Hence the entire term vanishes! Another excellent way to look at the vanishing of the triple product is to remember that the volume of the parallelepiped formed by three vectors will vanish if they are linearly dependent. And, of course,
. These two are perpendicular vectors! Hence the entire term vanishes! Another excellent way to look at the vanishing of the triple product is to remember that the volume of the parallelepiped formed by three vectors will vanish if they are linearly dependent. And, of course, ![Rendered by QuickLaTeX.com [\bold{w,u,w}]=0](https://oafak.com/wp-content/ql-cache/quicklatex.com-ed0e93742d0d7feb28b0c9b7f22fb058_l3.png) because of linear dependence!
because of linear dependence!
In the square brackets,
I will appreciate it if the examples below are treated tomorrow..
examples: 2.9, 2.20, 2.26, 2.28, 2.29, 2.34, 2.38, 2.39…
That being said ,sir..Is it safe to say since we are not done with the chapter 2 part of this course yet,do we really have to go through the 100 solved examples to consider ourselves prepared for the forthcoming test…
I do not want it to sound as if i am giving excuses,sir;this course is very interesting and we are trying our best to take it slow and steady for better understanding..
Your interest in the problems selected is noted; yes, you will need to go through ALL of the questions in the chapter to be adequately prepared. If there are questions you cannot follow, ask them as soon as possible.
noted sir..
Are matrix and second ranked tensor the same thing
No, they are not the same. A tensor is necessarily a linear transformation of a vector to a vector. Every tensor has a matrix part and its bases dyads when expressed in component form. A tensor exists whether it is expressed in component form or not. There is a specific transformation relationship between the matrix form of a tensor in one set of bases to its matrix form in another. It is this relationship that makes it a tensor. Matrices do not require such transformations and relationships in order to qualify as matrices. Despite the fact that the second ranked tensor, in its matrix representation, sans the bases, looks like a matrix, despite the fact that the rules governing them and their properties are equipollent (determinant, trace, cofactor, etc.) they still are different structures.
The difference between the composition of tensors,tensor product and also the inner product of tensors.
I dont really get these clearly
T^2
T.T
T:T
And these too as well
Composition is defined on S7.16. Inner product is defined from S7.34. In our work, there is no operator for composition so that the composition of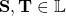 is written simply as
is written simply as 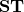 . Some textbooks write this as
. Some textbooks write this as 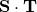 . We avoid that usage and adopt the convention that a single dot product, wherever it occurs, is always between two vectors. That simple rule makes things clearer.
. We avoid that usage and adopt the convention that a single dot product, wherever it occurs, is always between two vectors. That simple rule makes things clearer.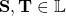 , which is the trace of the composition of
, which is the trace of the composition of 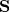 and the transpose of
and the transpose of 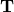 or the composition of the transpose of
or the composition of the transpose of 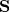 and
and 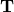 is written as
is written as
The operator for inner product is the colon symbol so that the inner product of
(1)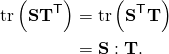
Squarring a tensor usually means a composition with itself. If, after carefully reading the definitions, you still have a specific question, I will answer you. However, I will stop approving your posts if you will not write in Latex and will not write your questions and scan them as I have advised you to do.
The text above was entered with Latex as follows: The spaces between e and x in the code [late x] … [/late x] are deliberate errors to prevent the following code from executing.
In our work, there is no operator for composition so that the composition of [late x]\bold{S,T}\in\mathbb{L}[/late x] is written simply as [late x]\bold{ST}[/late x]. Some textbooks write this as [late x]\bold{S}\cdot\bold{T}[/late x]. We avoid that usage and adopt the convention that a single dot product, wherever it occurs, is always between two vectors. That simple rule makes things clearer.
The operator for inner product is the colon symbol so that the inner product of [late x]\bold{S,T}\in\mathbb{L}[/late x], which is the trace of the composition of [late x]\bold{S}[/late x] and the transpose of [late x]\bold{T}[/late x] or the composition of the transpose of [late x]\bold{S}[/late x] and [late x]\bold{T}[/late x] is written as
[late x]
(2)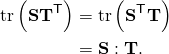
[/late x]
Good day sir; In chapter 2 question 27, is the cofactor and determinant of a tensor product always 0? if yes, how did they come to that conclusion? like can it be proved.
First of all, it is a straightforward matter to show that the determinant of a dyad is ALWAYS zero: Let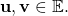 By definition, Let there be linearly independent
By definition, Let there be linearly independent 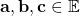
(1)![Rendered by QuickLaTeX.com \begin{align*} \det({\bold{u}\otimes \bold{v}})&=\frac{\left[\bold{(\bold{u\otimes v})a,(\bold{u\otimes v})b,(\bold{u\otimes v})c}\right]}{\left[\bold{a,b,c}\right]}\\ &=(\bold{v\cdot a})(\bold{v\cdot b})(\bold{v\cdot c})\frac{[\bold{u,u,u}]}{\left[\bold{a,b,c}\right]}\\ &=0 \end{align*}](https://oafak.com/wp-content/ql-cache/quicklatex.com-9d73c947ea75610ee77268ba248dadad_l3.png)
because of linear dependence. The determinant of the dyad is zero.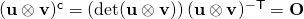 on account of the vanishing of the determinant, so that the cofactor of the dyad is also zero.
on account of the vanishing of the determinant, so that the cofactor of the dyad is also zero.
Second, remember that the
Ohh… Thank you Sir.
Sir although I looked at the questions is there any textbook that could be recommended for the dot and vector cross sums
Sir although I looked at the questions is there any textbook that could be recommended for the dot and vector cross sums
160407047