I didnt know it wasnt going to show the vectors and scalars.
in slide7 page 26 the solution you solved i dont understand how the denominator of the trace was removed
The denominator you are talking about is . That is the triple product of the three orthonormal base vectors. It is not a good sign that it is not already obvious to you that it is the volume of a cube with all sides equal to unity! On that basis alone, we can conclude that, . Another way to look at it is to remember that,
(1)
Furthermore, in Q&A 1.35 it was shown that,
(2)
Note that,
(3)
These four ways of seeing the result should be obvious to you from Week Two lectures. You need to go back and work through that in order to have a fighting chance in the exams.
You are NOT communicating! I do not know what you have in mind! Here are your choices:
1. Learn Latex and write your questions to me in Latex.
2. Write your questions by hand, denoting vectors with a bar, tensors with a double bar. Take a scan of the question on a Google drive and send a link to the scanned file.
If you are making a reference to a specific item treated in the book, slides, tutorials or programming clinics, use this reference strategy: Chapter 3, Page 34 equation 5 is self explanatory; S8.15 will mean the week 8 slides, page 15; Tutorial 3.46 is tutorial 3 page 46; PC3.5 is the programming clinic slide 3, page 5.
If you do not do any of these, you will need a witch to automatically know what is in your mind! I am not a witch!
tr ⊗ ≡ 1 ⊗
=( ⊗ 1 , 2, 3 + 1, ⊗ 2 , 3 + 1, 2, ⊗ 3) / (1, 2, 3)
I dont really understand how to get to the next step from the one above
=1/1(1, 2, 3 + 1, 2, 3 + 1, 3, 3)
= 1 ⋅ 23 + 31 ⋅ 2 + 12
⋅ 3
= 1 ⋅ 2311 + 3122 ⋅ 2 + 1233 ⋅ 3 =
= ⋅ v
I didnt know it wasnt going to show the vectors and scalars.
in slide7 page 26 the solution you solved i dont understand how the denominator of the trace was removed
The denominator you are talking about is![Rendered by QuickLaTeX.com \left[ \bold{e}_1,\bold{e}_2,\bold{e}_3\right]](https://oafak.com/wp-content/ql-cache/quicklatex.com-eff6f6e655553e245376fe12d29f262b_l3.png) . That is the triple product of the three orthonormal base vectors. It is not a good sign that it is not already obvious to you that it is the volume of a cube with all sides equal to unity! On that basis alone, we can conclude that,
. That is the triple product of the three orthonormal base vectors. It is not a good sign that it is not already obvious to you that it is the volume of a cube with all sides equal to unity! On that basis alone, we can conclude that, ![Rendered by QuickLaTeX.com \left[ \bold{e}_1,\bold{e}_2,\bold{e}_3\right]=1](https://oafak.com/wp-content/ql-cache/quicklatex.com-cfdae6bee19244688b00af74c570da23_l3.png) . Another way to look at it is to remember that,
. Another way to look at it is to remember that,
(1)![Rendered by QuickLaTeX.com \begin{align*} \left[ \bold{e}_1,\bold{e}_2,\bold{e}_3\right]&=(\bold{e}_1\times\bold{e}_2)\cdot\bold{e}_3\\ &=\bold{e}_3\cdot\bold{e}_3\\ &=1 \end{align*}](https://oafak.com/wp-content/ql-cache/quicklatex.com-3a504d421f241f4d03b5761b5e1f049b_l3.png)
Furthermore, in Q&A 1.35 it was shown that,
(2)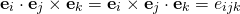
Note that,
(3)![Rendered by QuickLaTeX.com \begin{align*} \left[ \bold{e}_1,\bold{e}_2,\bold{e}_3\right]&=(\bold{e}_1\times\bold{e}_2)\cdot\bold{e}_3\\ &=\bold{e}_1\cdot\bold{e}_2\times\bold{e}_3\\ &=e_{123}\\ &=1 \end{align*}](https://oafak.com/wp-content/ql-cache/quicklatex.com-a1c3a4700d438653d84731f8977e8c52_l3.png)
These four ways of seeing the result should be obvious to you from Week Two lectures. You need to go back and work through that in order to have a fighting chance in the exams.
You are NOT communicating! I do not know what you have in mind! Here are your choices:
1. Learn Latex and write your questions to me in Latex.
2. Write your questions by hand, denoting vectors with a bar, tensors with a double bar. Take a scan of the question on a Google drive and send a link to the scanned file.
If you are making a reference to a specific item treated in the book, slides, tutorials or programming clinics, use this reference strategy: Chapter 3, Page 34 equation 5 is self explanatory; S8.15 will mean the week 8 slides, page 15; Tutorial 3.46 is tutorial 3 page 46; PC3.5 is the programming clinic slide 3, page 5.
If you do not do any of these, you will need a witch to automatically know what is in your mind! I am not a witch!