We continue the application of differential calculus to tensor objects. This lecture begins with a review of limits and derivatives with its extension to large objects.
[gview file=”http://oafak.com/wp-content/uploads/2019/10/Week-Eleven-3.pdf”]
We note that online participation is improving. Keep it up!
Good morning sir,
I dont quite understand higher order tensors such as 3rd,4th and so on
160404050
We do not really require knowledge of such higher order tensors in this course. The exception is the Levi-Civita Tensor that was introduced in its triad components in Week 11 lecture. That should be easy to understand.
Good day. I wanted to inquire as to gain more knowledge on the applications of Vectors, Tensors, invariants, Field, and lots of other functions and theorems learnt in this course to real life problems. Mrs. Adewunmi gave us an example of Fluid flow in pipes and stated we could also use the knowledge in writing our final year projects and coding later on. Are they more to add to the list?
160404036 Mechanical Engineering
A number of examples have been given in the first three chapters. More will come in subsequent chapters.
Thank you, sir. Well noted.
You are welcome
A sample question, please see the linked file below:
https://drive.google.com/open?id=16U-e0ZyeLvihXBkD2O0HwWxH-DO8vWbb
While studying the Week 11 lecture slide 9, I noticed lim →0[(
+ + − + + + − )/] was simplified to;
lim →0
[ ( + ) − ()]/ (1)
+ lim →0
[ ( + ) − ()]/ (2)
Is the ‘y’ in the eqn (1) a mistake? because I don’t understand what brought about it
160404015 Mechanical Engineering
Just look two lines below where you are talking about. The definition,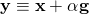 is given there. If you replace the RHS with
is given there. If you replace the RHS with 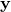 in this expression, the result becomes immediately clear.
in this expression, the result becomes immediately clear.
Next time you want to comment, you either learn to use Latex or make a scan of your written question into a google drive and send the url as Emmanuel did above. It not hard to do Latex.
In order to show you some Latex codes, I will be appending the latex codes of my responses from now on. Here is the above reply exposing the latex code:
Just look two lines below where you are talking about. The definition, \bold{y}\equiv\bold{x}+\alpha\bold{g} is given there. If you replace the RHS with \bold{y} in this expression, the result becomes immediately clear.
Also from week 11 lecture slide 16
ቤ tr d/da( S + adS)= tr(IdS)
=0
I understand that at limit a-> 0, adS=0
leaving d/da(S) which should still be equal to zero, but on the slide is tr(IdS).
I don’t understand how the result was obtained
160404015 Mechanical Engineering
You are differentiating with respect to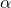 . When you do, only things containing
. When you do, only things containing 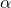 survive. You therefore have,
survive. You therefore have,
(1)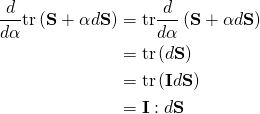
The identity tensor enters the equation and remember that it changes nothing. Then remember that the trace of the product of a tensor and the transpose of another is the inner product. Lastly remember that the transpose of the identity tensor is the identity tensor itself!
(1)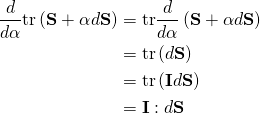
Thank you sir, fully understood.
Please sir I would like to understand why in rigid body dynamics the inertia matrix is often referred to as the inertial tensor,is this a valid claim or a misuse of the term since we have not established a basis for the inertia matrix
160407029 Systems Engineering
It is a tensor! The Moments of Inertia are the diagonal terms, the Products of Inertia are the off diagonal terms. It is also symmetric in that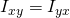 . It is a second-order tensor. Its full properties cannot be fully discussed because of the late introduction (if at all) of tensor algebra!
. It is a second-order tensor. Its full properties cannot be fully discussed because of the late introduction (if at all) of tensor algebra!
Good day sir, please can you explain more about a mixed tensor
We avoided general tensors that will necessitate discussions on covariant, contravariant and mixed tensors at this level. If you want to discuss such advanced matters, let me know how much you have done on it first.
Okay sir
Thank you
Pls can you provide an intuitive example of a big object(tensor) changing with respect to another big object I.e what can the derivative of a tensor with another tensor represent physicaly
160407029 Systems Engineering design
Stress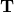 is a second-order tensor. So is strain as can be measured by
is a second-order tensor. So is strain as can be measured by 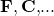 for Deformation Gradient, Right Cauchy-Green Tensor, …. For any material, the stress field is attended by a strain field. Clearly
for Deformation Gradient, Right Cauchy-Green Tensor, …. For any material, the stress field is attended by a strain field. Clearly 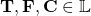 are such that,
are such that,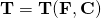 is a tensor-valued object of tensor fields.
is a tensor-valued object of tensor fields.
The nature of this relationship varies from material to material. The study of this especially for new materials is perhaps the most active field of research in Continuum Mechanics. It is called Constitutive Theory. Constitutive relations are not restricted to stresses. They include temperature, heat rates, deformation and strain gradients. One example is the Piola Referential Stress,
(1)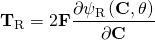
In an isothermal case, for small deformations, we may have,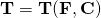
You can take the gradient of this field with respect to the arguments of the field. That is an example of what you want to know, is it not. For example, you may want to look at page 342 in the book: The Mechanics and Thermodynamics of Continua by Gurtin, Fried and Anand. (full ref at the end of Chapter 3 text) One of the goals of this course is to make such materials within your reach.
Here is the input that produced the earlier reply. I deliberately included an error in the spelling of “latex” as “late x” to prevent the code from execution:
Stress [late x]\bold T[/late x] is a second-order tensor. So is strain as can be measured by [late x]\bold {F, C,} …[/late x] for Deformation Gradient, Right Cauchy-Green Tensor, …. For any material, the stress field is attended by a strain field. Clearly [late x] \bold {T, F, C}\in \mathbb{L}[/late x] are such that,[late x]\bold {T=T(F,C)}{[/late x] is a tensor-valued object of tensor fields.
The nature of this relationship varies from material to material. The study of this especially for new materials is perhaps the most active field of research in Continuum Mechanics. It is called Constitutive Theory. Constitutive relations are not restricted to stresses. They include temperature, heat rates, deformation and strain gradients. One example is the Piola Referential Stress,
[late x]
\begin{alig n}
\bold{T}_\textrm{R}=2\bold{F}\frac{\partial \psi_{\textrm{R}}\left(\bold{C},\theta\right)}{\partial\bold{C}}
\end{alig n}
[/late x]
In an isothermal case, for small deformations, we may have, [late x]\bold{T=T(F,C)}[/late x]
You can take the gradient of this field with respect to the arguments of the field. That is an example of what you want to know, is it not. For example, you may want to look at page 342 in the book :The Mechanics and Thermodynamics of Continua by Gurtin, Fried and Anand. One of the goals of this course is to make such materials within your reach.
Pls sir while looking into some examples of physical tensors I came across a text that claims engineering strain is not a tensor even though it looks like one is this a valid claim.
Drive link to page excerpt is given below
https://drive.google.com/file/d/12jTVCoAgi3PI8HHK4sb6A2PU1GzqqcWb/view
160407029 systems engineering
“Looks like one” is the key here. That is the reason you spent so much time on what a tensor really is. There are several measures of strain that you will come across. Anything that does not meet the transformation requirements that we have defined is not a tensor. There are other quantities that are in use that are not tensors. The linear strain defined as increase in length over original length, will also not meet the strict rules and can be said to be “not tensor” also. It is an approximation to the Lagrangian and the Eulerian strains – both are strain tensors. These approximations are valid when the deformations are small.We already have the tools to do study why these can be tensors and whether it even matters. We will be able to see what makes a function a proper strain tensor function. I will post chapter four soon. These matters are discussed more deeply there.
In 3 dimensional Euclidian space, a rank 1 tensor is represented with a vector, a rank 2 tensor is represented with a 3×3 matrix, a rank 3 tensor is a 3x3x3 sized three dimensional array and so on. Assuming we are in 3 dimensional space, for example, is it possible to have an arbitrary sized matrix; say 6×7 sized matrix as the representation of a tensor? Or can they be only represented with arrays with dimensions of three’s powers?
Physical space is three dimensional. That is what mostly interests engineers. Higher dimensional space have analytical properties that interest many physicists and mathematicians. Tensors in the latter can have the kinds of matrix representation you imagine. Those are not our primary concern.
Alright sir thank you sir