We hereby present tutorial three as a correction rearrangement, in slides of most of the Q&A in chapter 3 of Continuum Mechanics for Modeling Simulation and Design.
[gview file=”http://oafak.com/wp-content/uploads/2019/10/Tutorial-Three01-1.pdf”]
Obviously, these cannot be covered in a single tutorial class. We will select a number of these if a tutorial is needed before you semester exams.
Good day sir, i would like to confirm the date the self test would close
I think it will be available up till the exam day. It is to achieve three purposes: 1. Help you prepare for the exam, 2. Improve your Continuous Assessment grade, 3. Assist you in building your knowledge in Tensor Analysis in preparation to serious work in Kinematics – our next topic.
Marks from my courses MUST be earned! No free lunch!
That would be great thank you Sir.
sir what website are we using to carry out the self test.
ww.s2pAfrica.org is not showing the test option
http://masc.s2pafrica.org/
this the website
thank you
Good day Sir. Concerning the Exam, I would like to know the setup of the exam questions(theory or obj).
The only information I will give you for sure on the exam is that you do these things:
1. Learn from the several materials you have been given;
2. Work through all the examples in Q&A
3. Stop missing classes and do not keep looking for tricks to pass exams.
Of course number 3 is belated. If you understand the stuff, you will do well.
Thanks for the advice sir.God bless you abundantly
Good Day Sir, please can we get an updated version of chapter 2 Q&A, some answers are not explanatory, like Q2.5
Q2.5 is sufficiently explanatory. Ask a specific question on it if you need to. Chapter Two as published conforms to the latest that I have on file. If you have a difficulty with any other problem in that chapter, let your request for explanation be specific.
Good day sir, I tried the online test today around 12, it just stopped going suddenly when I was in question 15. I’m still going to do it 10 more times but I humbly request that you don’t assume my mark for today’s own
Send your Matriculation Number, Test ID (Chapter One, Two Or Three) and Time of Self Test with the above comments. The matter will be investigated and resolved accordingly.
160407050
Onasanya
Chapter 1
About 12pm yesterday
Good day sir, I tried the online test today around 12, and it suddenly stopped working while I was half way…
I will still do the test 10 more times, but please I humbly request that you don’t count today’s own as part of my mark.
See comments on the duplicate post.
Sir, please is it possible to find angles between dyads
Yes. Remember that a dyad is a tensor. Slide 8.8 tells you how to do this: Let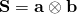 and
and 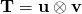 be two dyads, the angle
be two dyads, the angle 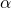 between them is
between them is
(1)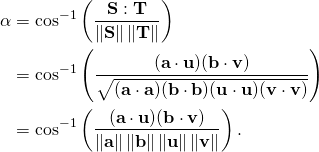
This is directly analogous to the situation of the angle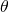 between two vectors
between two vectors 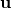 and
and 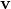 :
:
(2)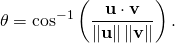
The analogy ends there as you cannot plot dyads or any tensor for that matter as straight lines with angles between them since the representation of directed lines for tensors do not exist. The algebraic analogy is all you get for this and higher order tensors in Euclidean vector spaces.
Sir, from trying to find out a little about tensors I want to know what the relationship between 3rd order tensor and the crossproduct.
Secondly:
Is there another space where tensors can operate/exist?
The cross product, defined between two vectors in 3D Euclidean Vector Space, can be entirely replaced by a tensor operation. Such a tensor can be formed by the contracting a third-order Levi-Civita Tensor,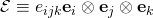 on any vector. For example, given any vector
on any vector. For example, given any vector 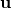 , the operation,
, the operation, 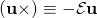 produces the second-order tensor called the Vector Cross of
produces the second-order tensor called the Vector Cross of 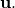 In component form, the vector cross can be expressed as,
In component form, the vector cross can be expressed as,
(1)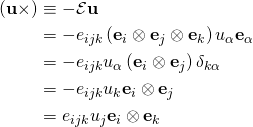
The cross product of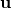 with any other vector
with any other vector 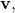 is the same as the vector cross acting on that vector:
is the same as the vector cross acting on that vector:
(2)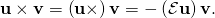
This is a tensor operation completely replacing the cross product!
Tensor of the second order can interact in any Euclidean Vector Space from zero order (scalars) to higher orders.
Good day sir, I would like to be enlightened more on how the volume integral of the divergence of a tensor field is related to the same vector field integrated over the surface. More emphasis on the formula prove.
First, you may want to look at some videos on divergence and curl of vectors. After that, you might want to look at a visual explanation of the Divergence Theorem.
OK. Would take out time to look at the videos. Thank you.
Good day sir, so today I tried to take a self test on chapter 1 but an error came out saying “you have no more attempts”. I would love to take another one.
Good afternoon sir,
I tried logging into the self test site to prepare for the exams but it keeps telling me I don’t have available attempts.
170407509
Systems Engineering
I experienced the same this afternoon when I tried to log into the self test
Check the information posted yesterday October 28. The self test should be open again today. Try again