Good day sir, the way you feel concern about this course is the way some of your students feel about it too. Going forward, I feel the self test should be made available as many as possible for students after every week classes, this will enhance the impactation you are trying to get into us. To be very sincere, it was after I took my second self test, I was able to solve some practical question. The self test is different from the practice question in the chapters in the sense that, the way the question is set is quite different from each other. It may be easy for other students but I find it hard to comprehend. Also after taken either the self test or the actual test, the ones missed should be marked out in particular so that we can make reference to the text and make corrections. ‘Cause after the test I’m always confused about which one I missed. In conclusion, I feel these process and changes stated above will improve the course as a whole. Thank you sir.
Good day sir. Please I would like to appeal if I can be given one more attempt with my Chapter one test. I had some foundational concepts wrong for this course, making me do a lot of miss-ups and mess-ups in the Chapter one test. One more trial would go a long way. An exception I don’t deserve but humbly ask for. Thanks.
Matric no 160407003 Systems Engineering
It was a great semester learning from you. Your efforts to make sure every students in the class understood helped the process for me. Thank you sir and your Team.
“so far so good” ,
this is one of the course we had a thorough break down of foundations.
hopefully we get more of this.
Thank you sir for your efforts.
It all ended well, It was a great semester learning from you sir. We sincerely appreciate your relentless effort during classes and tutorial most especially the breakdown to our very own level which you proved to is that it never too late to keep trying. Thanks so much sir
Your other comment has been trashed because it is not a serious comment as it did not complete the sentence!
Is a vector cross, invertible?
To answer this question, first observe that the cofactor of a vector cross, . Q2.29 shows that the third invariant,
Remember that the inverse of a tensor is, In the case of the vector cross, we can write that,
(1)
because this particular cofactor is obviously symmetrical.
Here you are dividing by zero so that the inverse is not defined. The vector cross is therefore not invertible. This is an example of a tensor that has a unique, computable cofactor but yet, it is not invertible because its determinant vanishes.
Good day sir, the way you feel concern about this course is the way some of your students feel about it too. Going forward, I feel the self test should be made available as many as possible for students after every week classes, this will enhance the impactation you are trying to get into us. To be very sincere, it was after I took my second self test, I was able to solve some practical question. The self test is different from the practice question in the chapters in the sense that, the way the question is set is quite different from each other. It may be easy for other students but I find it hard to comprehend. Also after taken either the self test or the actual test, the ones missed should be marked out in particular so that we can make reference to the text and make corrections. ‘Cause after the test I’m always confused about which one I missed. In conclusion, I feel these process and changes stated above will improve the course as a whole. Thank you sir.
You can take the tests now. It is opened and there are no restrictions
Thanks for your comments. It is a useful one. We will look at what we can do and which we can implement.
Thank you Sir
Good day sir. Please I would like to appeal if I can be given one more attempt with my Chapter one test. I had some foundational concepts wrong for this course, making me do a lot of miss-ups and mess-ups in the Chapter one test. One more trial would go a long way. An exception I don’t deserve but humbly ask for. Thanks.
Matric no 160407003 Systems Engineering
You can go to any chapter and test yourself again.
Thank you sir. This is a very impactful way of teaching
It was a great semester learning from you. Your efforts to make sure every students in the class understood helped the process for me. Thank you sir and your Team.
“so far so good” ,
this is one of the course we had a thorough break down of foundations.
hopefully we get more of this.
Thank you sir for your efforts.
My pleasure. I thoroughly enjoyed working with this set. I look forward to great things happening to you!
It all ended well, It was a great semester learning from you sir. We sincerely appreciate your relentless effort during classes and tutorial most especially the breakdown to our very own level which you proved to is that it never too late to keep trying. Thanks so much sir
It has been a great pleasure with 300 level student in the two departments.
Good day sir ,after the exam i came across something that got me confused and i would like to know, my question is , is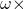
not invertible
Your other comment has been trashed because it is not a serious comment as it did not complete the sentence!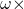
invertible?
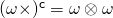. Q2.29 shows that the third invariant,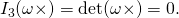 
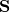is,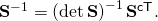 
In the case of the vector cross, 
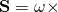we can write that,
Is a vector cross,
To answer this question, first observe that the cofactor of a vector cross,
Remember that the inverse of a tensor
(1)
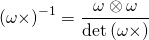
because this particular cofactor is obviously symmetrical.
Here you are dividing by zero so that the inverse is not defined. The vector cross is therefore not invertible. This is an example of a tensor that has a unique, computable cofactor but yet, it is not invertible because its determinant vanishes.
thank you very much sir