In week 6 (slide 23), it was stated that the tensor transforms linearly from one euclidean vector space to another. Does this mean that Euclidean spaces could be unique from one another? That is to say that the Euclidean vector space of the original vector is different from that of the transformed vector? If so, why the uniqueness? Is the euclidean space not singular and common to all vectors?
It is possible that the vector space of the input is the same as the vector space of the output; it is not necessarily so. Here is an example of the situation: Given a Cauchy stress tensor, you can transform the normal to a surface to its stress vector. In this case, the stress vector is the output while the normal is the input. It is obvious that we are dealing with two different vector spaces here: The one, a normal to a surface, dimensionless, the other, a stress vector, having the units of force per unit area.
The transformation rules applies whether the input vector is from the the same vector space as the output or not. You can say that a tensor maps a vector space unto itself, or to another vector space. You will be correct in either case.
Sir in Week Ten it was stated that the Liouville’s theorem was gotten from the basis of the derivative of the third invariant. Does the second invariant help provide any basis for a theorem.
160407047
Now, what really is a theorem? It is simply a result, important enough to be given a name! It is given a name, often related to the history of its derivation and/or discovery or related to the names of the persons related to that process. Once we agree with that basic meaning, then, of course, there are several results (call them theorems if you like) related to the second invariant! Off the bat, I can name a few:
1. The fact that the cofactor tensor transforms areas that have been transformed by the original tensor is a major result related to the trace of the cofactor. As you will remember that the second Invariant is a scalar function of the cofactor – the trace! This takes care of the area magnification when the tensor involved is the deformation gradient.
2. The fact that a rotation is self-cofactor means that its second invariant is exactly the same as the first invariant. Consequently, a rotation is fully known once either is first or second invariant is known as the third invariant is already known to be unity.
3. Cayley-Hamilton theorem tells us that the cofactoe of a tensor can still be extracted even when it is not invertible.
There may be other results that we did not name because we simply use them as they are either easily derived or are not of sufficient moment to be treated specially. Anytime a result is related to the cofactor, it is related to the second invariant.
The derivative of the cofactor, by itself, does not provide a useful result known to me.
The worked example Q2.30 shows exactly how . There are five steps in the proof. When I know which of the steps you find difficult, then I may be in a position to assist you.
Were you also able to reach the answer that way? If you were to write the tensor objects out i full, what you have written may not be possible. I have not tried it though.
In week 6 (slide 23), it was stated that the tensor transforms linearly from one euclidean vector space to another. Does this mean that Euclidean spaces could be unique from one another? That is to say that the Euclidean vector space of the original vector is different from that of the transformed vector? If so, why the uniqueness? Is the euclidean space not singular and common to all vectors?
It is possible that the vector space of the input is the same as the vector space of the output; it is not necessarily so. Here is an example of the situation: Given a Cauchy stress tensor, you can transform the normal to a surface to its stress vector. In this case, the stress vector is the output while the normal is the input. It is obvious that we are dealing with two different vector spaces here: The one, a normal to a surface, dimensionless, the other, a stress vector, having the units of force per unit area.
The transformation rules applies whether the input vector is from the the same vector space as the output or not. You can say that a tensor maps a vector space unto itself, or to another vector space. You will be correct in either case.
Ok. Thank you sir.
Sir in Week Ten it was stated that the Liouville’s theorem was gotten from the basis of the derivative of the third invariant. Does the second invariant help provide any basis for a theorem.
160407047
Now, what really is a theorem? It is simply a result, important enough to be given a name! It is given a name, often related to the history of its derivation and/or discovery or related to the names of the persons related to that process. Once we agree with that basic meaning, then, of course, there are several results (call them theorems if you like) related to the second invariant! Off the bat, I can name a few:
1. The fact that the cofactor tensor transforms areas that have been transformed by the original tensor is a major result related to the trace of the cofactor. As you will remember that the second Invariant is a scalar function of the cofactor – the trace! This takes care of the area magnification when the tensor involved is the deformation gradient.
2. The fact that a rotation is self-cofactor means that its second invariant is exactly the same as the first invariant. Consequently, a rotation is fully known once either is first or second invariant is known as the third invariant is already known to be unity.
3. Cayley-Hamilton theorem tells us that the cofactoe of a tensor can still be extracted even when it is not invertible.
There may be other results that we did not name because we simply use them as they are either easily derived or are not of sufficient moment to be treated specially. Anytime a result is related to the cofactor, it is related to the second invariant.
The derivative of the cofactor, by itself, does not provide a useful result known to me.
Sir how is the
cof(cof ) = (det )
Sir in question 2.3 how is the
cof(cof S) = (det S)S
for an invertible tensor.
The worked example Q2.30 shows exactly how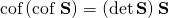 . There are five steps in the proof. When I know which of the steps you find difficult, then I may be in a position to assist you.
. There are five steps in the proof. When I know which of the steps you find difficult, then I may be in a position to assist you.
I think its pretty clear, the only confusion can come on the third line.
The third line is straightforward: Note that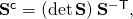 it is easy to see that the inverse of this is simply
it is easy to see that the inverse of this is simply 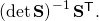 That is the essence of the third line.
That is the essence of the third line.
Hello Sir, on P2.38 why use the below matrix?
and not
Because if I take the determinant of the later matrix, it will give me the expression in the P2.38 (T + UFV)
Were you also able to reach the answer that way? If you were to write the tensor objects out i full, what you have written may not be possible. I have not tried it though.