[gview file=”http://oafak.com/wp-content/uploads/2019/09/Week-Seven-1.pdf”]
The slides are presented in two videos. Please note that these are still being edited.
The video continues …
[gview file=”http://oafak.com/wp-content/uploads/2019/09/Week-Seven-1.pdf”]
The slides are presented in two videos. Please note that these are still being edited.
The video continues …
Good day sir…sorry to take us back but in the Q&A 2.5 after getting Te1 and substituting v1 =1 ,v2=0,v3= 0.I’m a little confused as to why the coefficients of the result were compared with Te3 and not Te1
I suspect you have an old copy. There was an error. It has been corrected. Please look at the latest version at the webpage.
Good day sir, I want to ask why the principal invariants do not change and if it is possible to generate more invariants for a given tensor
There are other invariants that can formed for a tensor apart from the principal invariants that arise as coefficients of the characteristic polynomial. One such set is as follows: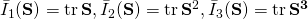 .
.
These are related to the principal invariants we have been using in this way:
(1)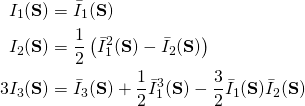
No matter how you define the invariants, they are related to the characteristic equation of the tensor. These are, in turn, independent of coordinate representation and are functions only of the tensors themselves. That is why they do not vary as you express the tensor in different coordinates. It is the same way a vector’s magnitude and direction are invariants for the vector.
You must not forget though that invariants are only a member of the important scalar-valued functions of the tensor. You can have many many such functions indeed.
Thank you very much for the insight, Sir
Sir, A deviatoric tensor is it necessarily skew? Why?
Areo Ajibola
170407512
Systems Engineering
In order to be sure you are not simply lazy, you first tell me what you know about a deviatoric tensor and a skew tensor. If after that you still have either of your two questions, I will answer one of them.
Thank you sir. I went back to the textbook and I saw the answer to my question. The deviatoric part of a Tensor depends on the original tensor it is taken.
Sir, it is also understanding the symbols’ meaning and implications that poses problem; but if I can have a material to help me have the fundamental and the basis knowledge, that would be good. I have not undergone the lecture before. Thanks.
Please see my previous answer.
Anyway, the info is rather cutting edge, so just like it.