Today is the last class on chapter one. I will still answer questions online on this chapter. Test is tomorrow, 11-1pm. Next week, we begin Chapter Two, Tensor Algebra. The goal of all you have learned in chapter one is to put you on a sound footing to learn tensor analysis. If you do chapter one well, the next chapter will be about the same or even easier. If you find the next chapter harder, it is likely coming from insufficient mastery of the material under vector analysis. Tensor theory is an extension of vectors.
[gview file=”http://oafak.com/wp-content/uploads/2019/08/Week-Five-3.pdf”]
We have added some of the materials that should have been covered in the Programming practice of yesterday.
Good evening sir,
If a•b×c = a×b•c ,
Why is it that (a×b)•(b×c)×(c×a) != (a×b)×(b×c)•(c×a)
I noticed that the RHS is (a×b•c)² from solved question 1.16 on page 78
But when the cross and the dot operator were interchange i.e (a×b)×(b×c)•(c×a) on the LHS we get (c×a•b)² which makes it not equal
But they are equal even as you wrote it! Remember that the square of a negative is the same as the square of a positive!
Thank you sir,
You mean
(a×b•c)² = -(b×a•c)² = (c×a•b)²
i.e
(a×b•c)² = (c×a•b)²
No. I do not mean that at all! I am worried about “you mean” in your statement. Exact Science is NOT a matter of opinion, or “you mean”. You should establish these things for yourself not just because I said so! At this stage, it should be easy, for example, for you to prove that only a sign separates the expressions; that is, use one of several methods to establish for a fact that,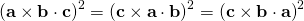 . This is because,
. This is because, 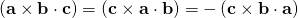 . A swap of the dot and the cross will not change sign, and every cyclic permutation retains sign. That is the reason why the product is written as,
. A swap of the dot and the cross will not change sign, and every cyclic permutation retains sign. That is the reason why the product is written as, ![Rendered by QuickLaTeX.com \left [ \bf a , b , c \right] \normalfont = \left [ \bf c, a , b \right]\normalfont = - \left [ \bf c, b , a \right]\normalfont](https://oafak.com/wp-content/ql-cache/quicklatex.com-b08a5b2221497742e55ee75534444dde_l3.png) . See, for example, problem 1.32 on page 85 in the Solved Problems section in the course textbook!
. See, for example, problem 1.32 on page 85 in the Solved Problems section in the course textbook!
Now I can comprehend
Thank you sir
• For rule #2, note that a zero vector will be represented by a
point; no length – resulting in a magnitude of zero. The negation
of a vector is simply to retain the direction but change the sense
of the arrow
I dont really get the part that negation of a vector only changes the sense but the direction
We define direction by the unit vector along a particular path. Every vector parallel to the unit vector is in that same direction. These are obtained by multiplying the vector by a scalar. When you use a negative scalar, you get the same direction but opposite sense. This idea of magnitude, direction and sense is shown graphically in S1.20.
Good evening sir
From the relationship ,
a.v=b.v ,concluding that a=b
Is this due to the relationship between the arbituary vectors or due to the fact that they are linearly independent
Tell me which particular step of 1.5 and 1.6 you do not understand. You question is already answered there!