Chapter two of the course text is posted here for your use. It is our hope that you will make use of this material given to you this time. Most students ignored the materials, turned deaf ears to all warnings and reaped the expected results in the test! The second chapter will be no different. Here, as before, there are 100 solved problems that are being turned into Multiple-Choice Questions. You will be examined on them within four weeks of today. We are working on the Web server that will allow you to also self test. [gview file=”http://oafak.com/wp-content/uploads/2019/08/Chapter-2.-Tensor-Algebra-7.pdf”]
We will cover some outstanding materials, hopefully, during the Programming class. We also include some guidance on the Q&A problems that are relevant to the week’s slides. If you work through them weekly, it will make the rush to cover the 100 questions unnecessary when the time for testing is near. Remember, these are mere guides. They are not to constrain you.
[gview file=”http://oafak.com/wp-content/uploads/2019/08/Week-Six-2.pdf”]
The same set of slides can be seen in the following video:
As in the past, we urge you to make your comments on these notes. Include information on your department and Matric number because we will grade your participation on the website as part of your Continuous assessment. The full details for the course grading are as follows:
[gview file=”http://oafak.com/wp-content/uploads/2019/08/Course-Grading-1.pdf”]
Good morning sir. Trust this meets you well. I recollect this test question but I have not been able to understand how to solve it sir. It says ‘Given a and b are vectors, we should explain (a+b)x(a-b).(bxa) . I would bevery glad if you could explain it sir as I could not answer it in the test.
Have you looked at Q1.16 in the course textbook, Chapter One? This question was based on it. It is a good idea to first look at the materials already given to you before asking a question. If after you have done that, you still have problems, I will be more than glad to help you.
Good morning, sir. On this new chapter on tensor. What exactly is a Tensor? I understand it is a linear transformation of a vector to another vector. Does this mean that tensor is an operator? But there is still something like ‘second order tensor(vectors)’ Is there any other way to describe a tensor?
Chiedozie Chika-Umeh 160404046
When we say “Tensor” with no qualifications, we are talking about a second-order tensor. The slides as well as the Course text say that at the outset. If we want to talk about any other kind of tensor, we would say so explicitly. A second-order tensor is a linear transformation from one vector space to another vector space.
We can write the tensor in an operator form, or in a functional form. For our use, it really does not make any difference. If you program in C++, for example, you will see that the only real difference between an operator and a function is not what actually gets done, but rather the syntax of invocation.In the way most texts present it, a tensor is presented in the operator form. However, there is nothing preventing it from being presented in a functional form.
After we have defined the tensor as a transformation, this week, we are exploring the implications of this definition in providing us induced attributes of a tensor. Those include its components, invariants, products (scalar products, compositions, tensor products and you already know the contraction with a vector which was the defining attribute. These together concretize what really a tensor is. Pay attention, read the materials you have. You appear to be a perceptive person who wants to learn. I think we can have a fair amount of discussion.
In the text, Vectors were differeciated from scalars by writing them in BOLD. In my note, I represent a vector ‘a’ by ‘a’ with a dash above it.
On getting to Tensor components, there’s a need to differentiate the tensor symbol T from its scalar components Tij when writing it down.
If I use a T with a dash above it, someone might take it as a Vector in a place where it is not. I know that a vector is a Tensor but I would like to know if there’s a generally acceptable way of writing the Tensor symbol?
Daniel I. Sumah
170404517
Mechanical Engineering.
If you want to write your equations by hand, you could use the double underlining to represent tensors: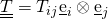 or, overlining, like this:
or, overlining, like this: 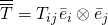 . This is the way people wrote before computers became common. But we are discussing in 2019! This is not 1974! Why on earth do you want to resort to the way we did things when I was an undergraduate? Why are you not finding out how I communicate with your class? It is NOT hard for you to learn the same tools that I use: Tex, Latex, Mathematica or even the Equations editor of Microsoft Word.
. This is the way people wrote before computers became common. But we are discussing in 2019! This is not 1974! Why on earth do you want to resort to the way we did things when I was an undergraduate? Why are you not finding out how I communicate with your class? It is NOT hard for you to learn the same tools that I use: Tex, Latex, Mathematica or even the Equations editor of Microsoft Word.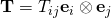 ?
?
Do you not prefer that the above expression looks like this:
Any of the software listed will give you the ability to write your equations with the same standard as your textbooks, my notes and slides! You can learn these things now rather than later!
Good Evening Sir, please when would the self test for last week be open for us to attempt?
The computer self test is still being programmed for a web server. I cannot guarantee when it will be ready. We are working hard on it. You can test yourself against the 100 problems that you have been given. Its essentially the same but in a different format.
Good day sir
Please I would like to ask, what is the spherical part in a tensor ?
Since a tensor without the spherical part is a deviatoric tensor.
Is it the spherical transformation?
NWANKITI UGOCHUKWU
160404017
Mechanical Engineering
Wait for the slides and video of Week 8. The same information you seek can be found on pages 14 and 15 of chapter 2.
Good day sir
Please can we get solutions to the test questions, i seem not to understand all.
Test questions are selected from the one hundred solved problems in the course text that you have been given! What you faced as an individual is a random selection.
Good evening sir,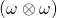 in the co-factor of
in the co-factor of 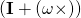 in question 2.26?
in question 2.26?
Please could you shed more light as to how you got the dyadic product
Uwadoka Okwesilieze
160404035
Mechanical Engineering
Take a look at 2.33 in the Q&A. You will see that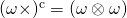
Good afternoon sir.
From Q&A 2.5a,
(After solving in class with Mrs.Adewumi,The first column of the Tensor was 1,2 and 3 not 3,-1,-1 as written in the text)
For 2.5a, There exist a relationship between the transformed basis vectors and the Tensor that transformed them.
The coefficient of e1,e2 and e3 for Te1,Te2 and Te3 respectively are the elements of column 1,2 and 3 of the transformation tensor(Tij values).
Will it be right say that this relationship will always exist when basis vectors are transformed by a tensor or is there a unique property of the tensor that makes this to happen?
SUMAH, Daniel Isunoya.
170404517
Mechanical Engineering
There are typographical errors in the answer to 2.5. They have been corrected.
If I understand your question well, you are implying you do not understand how a tensor transforms a vector. I will advise you to look again at the steps in Q2.5 (download the latest) and the other examples in the chapter.
Good day Sir.
During my 2nd test, On top of each question were references to the Q.A the questions were set from. I had some questions from Q&As that was over 100 (e.g Q.A 2.108) but there were only 100(99, actually) in the text.
I was able to answer them and I’ve downloaded the text multiple times to check if the text has been updated but Chapter 2 still has only 99 questions.
Should I expect an update to Chapter 2 even after we begin Chapter 3?
Sumah Daniel Isunoya
170404517
Mechanical Engineering.
Good day Sir,
Regarding Q.2.4b, I believe there is a shorter way to solve it.
If Tv = u x v [Taking u & v as vectors]
Then T(aw + bv) = u x (aw + bv)
= (u x aw) + (u x bv)
= a(u x w) + b(u x v)
= aTw + bTv [Implying T is a tensor]
where a & b are scalars.
You are correct; You have used the distributive property of the cross product over addition.
Good day sir,
is there a relation between spherical tensors and the spherical coordinate space?
No.
So sir, I have been thinking, are there tensors that are greater than rank 3 (the triads) and if so, how do we picture/imagine them as more dimensions will involved.
Are there any practical applications to these kind of tensor or they are just confined to the books alone(theoretical)
There are no geometric interpretations for higher-order tensors. However they exist often in analyses and they have algebraic meanings. One good example is the fourth-order elasticity tensor that relates stress to strain; if you differentiate a second-order tensor with respect to another second-order, you get a fourth-order tensor. These tensors have analytical applications. There are yet higher-order tensors also. If you give me a practical application of a first-order tensor, then I will supply a practical application of the fourth-order. Then we shall be on the same page on the meaning of “practical”.
Good day sir,
In Chapter 2 , Page 11 , Line 18
= : ( ⊗ )
Is it safe to say that = (: ( ⊗ ))( ⊗ )
Naomi, I edited your post as follows. I deliberately introduced a space in a keyword to prevent this from executing just to show you the way to input things in Latex for greater readability:
Good day sir,
In Chapter 2 , Page 11, Line 18
[l atex]
(1)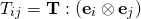
[/l atex]
Is it safe to say [l atex]\bold{T} =\left( \bold{T}:(\bold{e}_i \otimes \bold{e}_j )\right)(\bold{e}_i \otimes \bold{e}_j)[/l atex]
Good day sir,
In Chapter 2 , Page 11, Line 18
(1)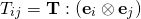
Is it safe to say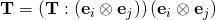
Yes, Naomi, you are correct. Just like it is also correct to say that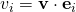 . We can proceed to say that
. We can proceed to say that  .
.
You can see the perfect analogy between vectors and tensors: You want components, you take scalar products with the bases; You want a component representation, you use the components you have calculated as coefficients of the bases. By following these analogies, you can transfer much of your vector analysis knowledge to tensors. Once you do so, you will lose your fear of tensors and see that it is simply an extension of your vector analysis. I am sure you can now see the futility of trying to learn tensors without knowing vectors!
Yes sir. Thank you
Good day sir,
In chapter 1, It was stated with prove that orthonormal sets are linearly independent but why is that not all linearly independent sets are orthonormal.
This question is easily answered: Take a linearly independent orthonormal set of vectors. Multiply one of them by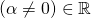 . The set remains linearly independent despite the fact that it is no longer orthonormal. It is clear that orthonormality is a sufficient condition for linear independence but not necessary. If a man wins the Olympic gold medal, it proves conclusively that he is alive and well. But you don’t even need to compete in the Olympics to be alive and well!
. The set remains linearly independent despite the fact that it is no longer orthonormal. It is clear that orthonormality is a sufficient condition for linear independence but not necessary. If a man wins the Olympic gold medal, it proves conclusively that he is alive and well. But you don’t even need to compete in the Olympics to be alive and well!
Good morning sir,
In chapter 1 page 30,Is it a must I use the third row to expand the matrix,because I try using the first row and it was not giving me the same answer of when the third row is used to expand the matrix
You can use any row or column to expand a matrix. If the answer is not the same, then you are doing something wrong. You will need to work the terms to the simplest forms to make comparisons correctly though.
Good morning sir
In Chapter 2, Page 13, The Last line
(1)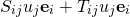
The same equation equals
Sir can you please explain how it so because there’s no dyad sign that implies a Tensor component
Naomi Inyang
170407509
Systems Engineering
The dyads are there in the earlier lines. The operation of the dyad on the vector was already carried out on the third line! There is no further explanation to give!
Good morning sir
In Chapter 2, Page 13, The Last line
(1)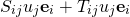
The same equation equals
Sir can you please explain how it so because there’s no dyad sign that implies a Tensor component
Naomi Inyang
170407509
Systems Engineering
Ohhh.. It acted on the vector u
I also could not get the T in the first equation to show using Latex although I typed it in
Ohhh.. It acted on the vector [latex] /bold{u} [\latex]
I also could not get the T in the first equation to show using Latex although I typed it in
Good morning sir, this question was given in this form [(
c) ×] = ( ×) and the answer was also given but i still didnt understand some of the steps that were followed to arrive at the final answer which is ( ×)
Question2.9 to be precise
Alas, you are NOT precise at all! The problem you are talking about is repeated on page two of Tutorial Two. I have counted 15 equations there. When you ask as you have done, are you telling me to repeat the 15 equations? How will that help you? In order to be specific, you will have to tell me which particular step you have not been able to follow.
Good morning sir
Is there a direct relationship between the identity tensor and the orthogonal tensor?
The determinant of an orthogonal tensor is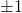 . When it is proper orthogonal, its determinant is
. When it is proper orthogonal, its determinant is 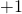 . For an identity tensor, the determinant is
. For an identity tensor, the determinant is 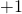 . We can view an identity tensor as a proper orthogonal tensor. That is quite technical. An orthogonal tensor leaves the magnitude of the vector it transforms unchanged. An identity leaves everything unchanged in a vector it transforms: magnitude and direction. I would rather have you stay with the definitions of these two structures and not get yourself confused with looking for similarities as their definitions are simple enough to understand.
. We can view an identity tensor as a proper orthogonal tensor. That is quite technical. An orthogonal tensor leaves the magnitude of the vector it transforms unchanged. An identity leaves everything unchanged in a vector it transforms: magnitude and direction. I would rather have you stay with the definitions of these two structures and not get yourself confused with looking for similarities as their definitions are simple enough to understand.
Good day sir…..pls in Chapter 2 question 2.51. I followed the solution for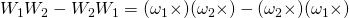
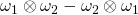
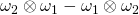
and got:
I don’t clearly get how it became:
Thanks for the question. The answer is correct. There is a typographical error in the premise of the solution. It should read thus: Given that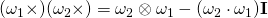 , show that,
, show that,
(1)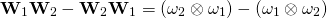
where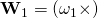 and
and 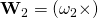 .
.
Goodday sir, what are ROTATIONAL TENSORS and are all ORTHOGONAL TENSORS ROTATIONAL??
Of the severel materials that you have apparently not been paying sufficient attention to, S8.32-34 directly answers your question here. We call it “Rotation Tensor”. It is a proper orthogonal tensor. Only propoer orthogonal tensors are rotation tensors.
Good morning sir, pls i don’t understand how you got your answer in chapter 2(Tensor Algebra) Q and A 2.79.
You mean you do not know how to find the tensor product between two tensors? It is an outer product: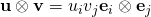 . The TensorProduct command in Mathematica can also be used.
. The TensorProduct command in Mathematica can also be used.
Sir I don’t understand how S^-c equals (detS)^-1S^T
By definition,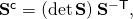 it is easy to see that the inverse of this is simply
it is easy to see that the inverse of this is simply 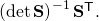
Good afternoon sir. Its quite a while. This is Ibikunle ‘Rotimi Adedayo; from Landmark University Omu-Aran. I really want to follow your lectures, by God’s grace study and understand them. Nevertheless I need what will introduce me to the preliminaries, to understand all the symbols involved in each lecture, the meanings, their significances and implications before going into the topics. This is about tensors, the properties and others.
This course has a specific strategy that builds the material from Week One (on Vector Analysis) up to Week Twelve. The material builds up slowly. All the symbols and terminology are fully explained in sequence. If you begin at Week One, I am sure following the later materials will not be a problem.